Рекурсивни функции в математиката

            Ако в дефиницията на някаква функция се използва самата функция, дефиницията на функцията е рекурсивна.

Примери:

а) Ако n е произволно естествено число, следната дефиниция на функцията факториел

е рекурсивна. Условието при n = 0 не съдържа обръщение към функцията факториел и се нарича гранично.

            б) Функцията за намиране на най-голям общ делител на две естествени числа a и b може да се дефинира по следния рекурсивен начин:

Тук граничното условие е условието при a = b.

            в) Ако x е реално, а n – цяло число, функцията за степенуване може да се дефинира рекурсивно по следния начин:

В този случай граничното условие е условието при n = 0.

г) Редицата от числата на Фибоначи

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...

може да се дефинира рекурсивно по следния начин:

В този случай имаме две гранични условия – при n = 0 и при n = 1.

            Рекурсивната дефиниция на функция може да се използва за намиране стойността на функцията за даден допустим аргумент.

            Примери:

            а) Като се използва рекурсивната дефиниция на функцията факториел може да се намери факториелът на 4. Процесът за намирането му преминава през разширение, при което операцията умножение с отлага, до достигане на граничното условие 0! = 1. Следва свиване, при което се изпълняват отложените операции.

            4! =

            4.3! =

            4.3.2! =

            4.3.2.1! =

            4.3.2.1.0! =

            4.3.2.1.1 =

            4.3.2.1 =

            4.3.2 =

            4.6 =

            24

            б) Като се използва рекурсивната дефиниция на функцията gcd, може да се намери gcd(35, 14).

            gcd(35, 14) =

            gcd(21, 14) =

            gcd(7, 14) =

            gcd(7, 7) =

            7.

В този случай няма разширяване, нито пък свиване. Двата аргумента на gcd играят  ролята на натрупващи параметри. Те се променят докато се достигне граничното условие.

            в) Като се използва рекурсивната дефиниция на функцията за степенуване може да се намери стойността на 2^-4.

 г) Чрез рекурсивната дефиниция на функцията, генерираща редицата на Фибоначи, може да се намери fib(5). 

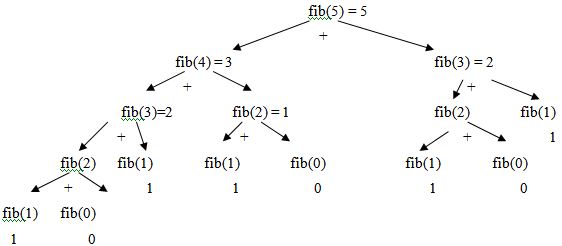
В този случай намирането на fib(5) генерира дървовиден процес. Операцията + се отлага. Забелязваме много повтарящи се изчисления, например fib(0) се пресмята 3 пъти, fib(1) – 5 пъти, fib(2) - 3 пъти, fib(3) – 2 пъти, което илюстрира неефективността на този вид пресмятане.

2.       Рекурсивни функции в C++

Известно е, че в тялото на всяка функция може да бъде извикана друга функция, която е дефинирана или е декларирана до момента на извикването й. Освен това, в C++ е вграден т. нар. механизъм на рекурсия – разрешено е функция да вика в тялото си самата себе си.

Функция, която се обръща пряко или косвено към себе си, се нарича рекурсивна. Програма, съдържаща рекурсивна функция е рекурсивна.

Чрез пример ще илюстрираме описанието, обръщението и изпълнението на рекурсивна функция.

            Пример за рекурсивна програма

            Задача 85. Да се напише рекурсивна програма за намиране на m! (m е дадено естествено число).

Програма Zad85.cpp решава задачата. 

Program Zad85.cpp

#include

int fact(int);

int main(){

cout << "m= ";

}

В тази програма е описана рекурсивната функция fact, която приложена към естествено число, връща факториела на това число. Стойността на функцията се определя посредством обръщение към самата функция в оператора return n * fact(n-1);.

            Изпълнение на програмата

Изпълнението започва с изпълнение на главната функция. Фрагментът

cout << "m= ";

int m;

cin >> m;

въвежда стойност на променливата m. Нека за стойност на m е въведено 4. В резултат в стековата рамка на main, отделените 4B за променливата m се инициализират с 4. След това се изпълнява операторът

cout << m << "!= " << fact(m) << '\n';

За целта трябва да се пресметне стойността на функцията fact(m) за m равно на 4, след което получената стойност да се изведе. Обръщението към функцията fact е илюстрирано по-долу:

            Генерира се стекова рамка за това обръщение към функцията fact. В нея се отделят 4B ОП за фактическия параметър n, в която памет се откопирва стойността на фактическия параметър m и започва изпълнението на тялото на функцията. Тъй като n е различно от 0, изпълнява се операторът

return n * fact(n-1);

при което трябва да се намери fact(n-1), т.е. fact(3). По такъв начин преди завършването на първото обръщение към fact се прави второ обръщение към тази функция. За целта се генерира нова стекова рамка на функцията fact, в която за формалния параметър n се откопирва стойност 3. Тялото на функцията fact започва да се изпълнява за втори път (Временно спира изпълнението на тялото на функцията, предизвикано от първото обръщение към нея).

            По аналогичен начин възникват още обръщения към функцията fact. При последното от тях, стойността на формалния параметър n е равна на 0 и тялото на fact се изпълнява напълно. Така се получава:

При петото обръщение към fact стойността на n е равна на 0. В резултат, изпълнението на това обръщение завършва и за стойност на fact се получава 1. След това последователно завършват изпълненията на останалите обръщения към тялото на функцията. При всяко изпълнение на тялото на функцията се определя съответната стойност на функцията fact. След завършването на всяко изпълнение на функцията fact, отделената за fact стекова рамка се освобождава. В крайна сметка в главната програма се връща 24 - стойността на 4!, която се извежда върху екрана.

            В този случай, рекурсивното дефиниране на функцията факториел не е подходящо, тъй като съществува лесно итеративно решение.

            Препоръка: Ако за решаването на някаква задача може да се използва итеративен алгоритъм, реализирайте го. Не се препоръчва винаги използването на рекурсия, тъй като това води до загуба на памет и време.

            Съществуват обаче задачи, които се решават трудно ако не се използува рекурсия.

Задача 86. Да се напише програма, която въвежда от клавиатурата записана без грешка формула от вида

            <формула> ::=  <цифра> |

                                            (<формула><знак><формула>)

            <знак> ::= + | - | *

            <цифра> ::= 0 | 1 | 2 | ...| 9.

Програмата да намира и извежда стойността на въведената формула (Например 8 --> 8; ((2-6)*4) --> -16).

Програма Zad86.cpp решава задачата.       В нея е дефинирана рекурсивната функция formula, реализираща рекурсивната дефиниция на <формула>.

Program Zad86.cpp

#include

int formula();

int main(){

cout << formula() << "\n";

            Забелязваме простотата и компактността на записа на рекурсивните функции. Това проличава особено при работа с динамичните структури: свързан списък, стек, опашка, дърво и граф.

            Основен недостатък е намаляването на бързодействието поради загуба на време за копиране на параметрите им в стека. Освен това се изразходва повече памет, особено при дълбока степен на вложеност на рекурсията.